Monty (CTM) and Three-Obsessed Monty (TOM). The presiding host is selected by a coin toss. The contestant starts by selecting Door 1. If the car is behind this door, Monty is assumed to open Door 3 with probability q; q = 1 2 for CTM and q = 1 for TOM. We suppose that Monty opens Door 3 to reveal a goat. For i = 1;2;3, let M. Les données de base du problème de Monty Hall : soient trois portes, cachant soit une chèvre soit une superbe voiture, l'automobile étant derrière une seule porte et les deux chèvres étant derrière les deux autres portes restantes.. Le problème de Monty Hall est une énigme mathématique [1], librement inspirée du jeu télévisé américain Let's Make a Deal.

The Monty Hall Problem Probability Mathigon

El problema de Monty Hall Colegio Mª Auxiliadora San Vicente

DJOE1 Le problème de Monty Hall YouTube

The Monty Hall dilemma explained easy 몬티홀 딜레마 쉬운설명! YouTube

[Math] Deal or No Deal Monty Hall Math Solves Everything

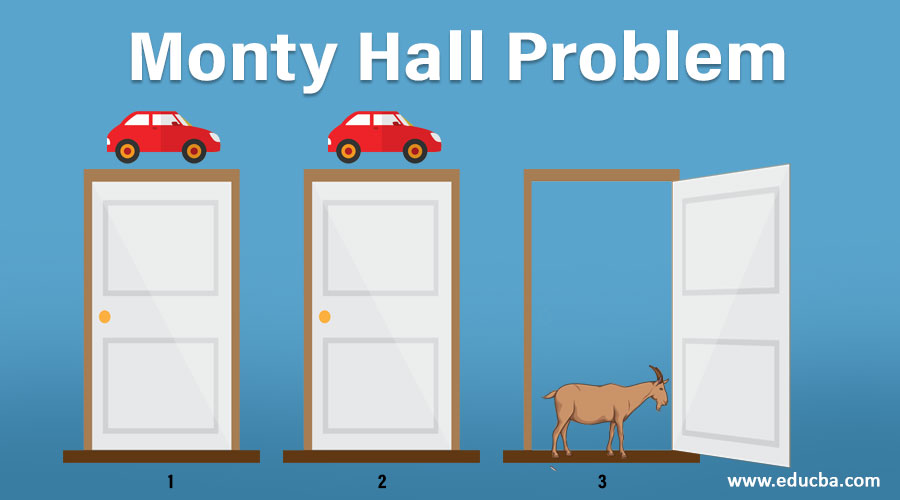
Monty Hall Problem Understand Monty Hall Problem in Detail

The Monty Hall problem YouTube

The Monty Hall Problem YouTube

Le problème de Monty Hall YouTube

Monty hall problem solved! YouTube

Le problème des 3 portes de Monty Hall YouTube

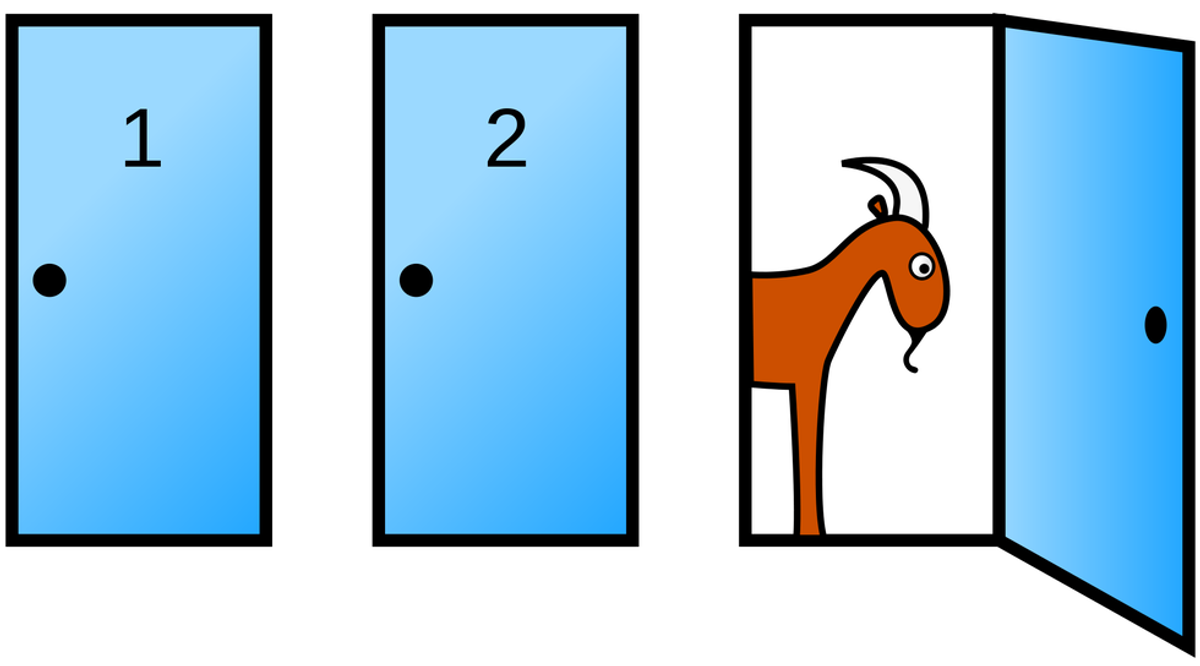
The Monty Hall Problem

The Monty Hall Problem Explained in Under a Minute YouTube

Solution Le jeu des trois boîtes, ou problème de Monty Hall Collectif de Recherche

Problema de Monty Hall Explicado sin Matemáticas Portal Friki

Problema de Monty Hall YouTube

Vidéo pop Le problème de Monty Hall Nagwa

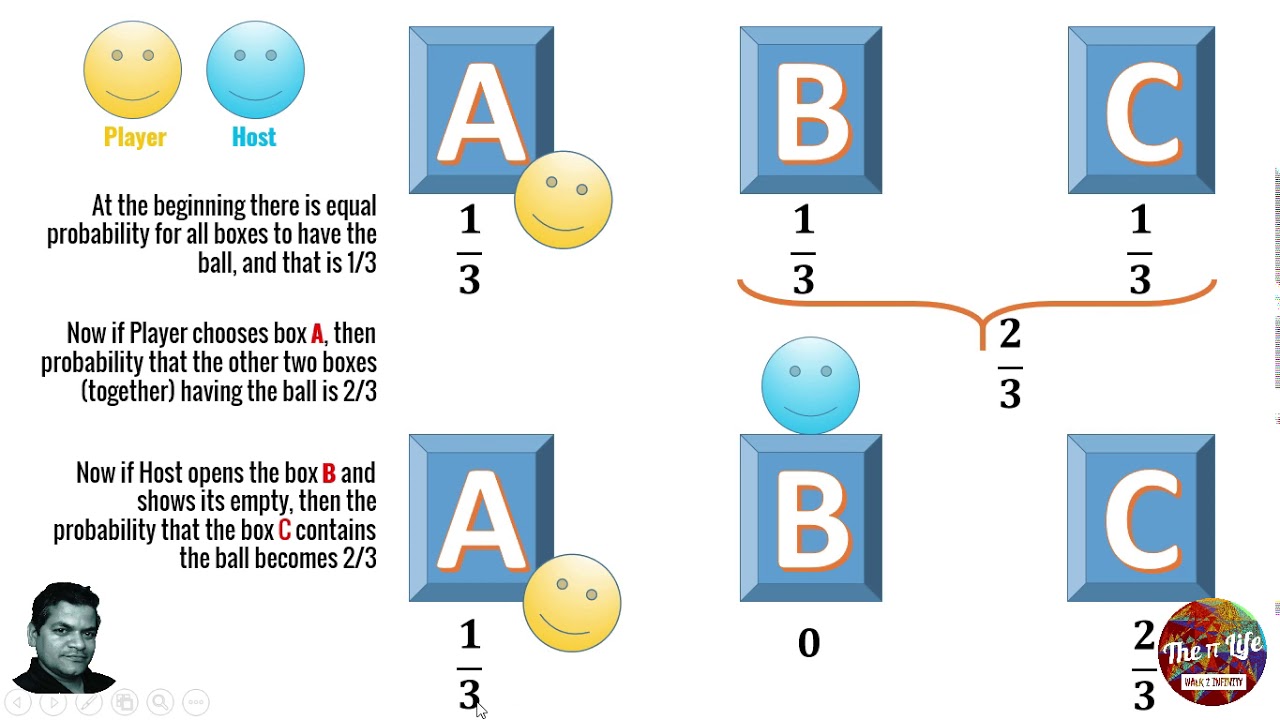
Monty Hall Problem A Game That Challenges Your Intuition. YouTube

Le paradoxe de Monty Hall (…disponible également en version « pigeon ») Science étonnante

Problème de Monty Hall

Le problème de Monty Hall est un problème probabiliste inspiré du jeu télévisé américain « Let's Make a Deal » et prend son nom du présentateur de l'émission. Voici les règles du jeu. Devant le candidat se trouvent trois portes. Parmi elles, deux portes ouvrent sur une chèvre et la dernière porte ouvre sur une voiture.. Solution du problème de Monty Hall, les trois portes. Étape 1 : Au debut, chaque porte a la même probabilité d'être gagnante, soit une chance sur 3, p=1/3. Considérons que nous choisissions la premiere porte, la voiture a 1 chance sur 3 d'être derriere la 1 ère et donc 2 chance sur 3 d'être parmi les 2 portes qui restent.